DenseNet Implementation On Stanford Dogs Dataset
Table of Contents
Introduction
This article is an analysis of the DenseNet Architecture described in the 2017 paper Densely Connected Convolutional Networks [1]. Each building block of the model will be analyzed. I'll also keep my notation consistent with the notation in the paper so that this article is easier to follow if read alongside the paper. For example, both this article and the paper will refer to the non-linear transformation associated with the layer of a network as .
The model will be trained on the Stanford Dogs Dataset, which contains 20,580 images categorized into 120 classes of dogs [2]. The architecture of DenseNets in general will be discussed, but the particular implementation shown will be for DenseNet121.
All of the models will use PyTorch. I also use Linux and I don't plan on making a Windows version of this blog. Frankly, if you're actually reading this and on Windows you are probably more than capable of translating any Linux commands to their Windows equivilant. To keep the code in this post more terse I've trimmed most of the docstrings from the various class and function definitions. The full code (including docstrings and instructions on running it) can be found on my GitLab repository.
Finally, this blog is not a replacement for reading the paper directly. You should read the paper before reading this blog in order to fully understand everything that is happening.
The Model
Overview
As convolutional neural networks continue to get deeper vanishing gradients become more problomatic. The DenseNet architecture attempts to aleviate this problem by making information from layers earlier in the network immediately available to layers deeper in the network. This architecture is heavily inspired by the ResNet architecture, in which a skip-connection is added, which adds the activation of the previous layer to the output of the non-linear transformation. This allows information from earlier in the network to flow forward more easily. This is represented as:
DenseNets also pass information from earlier in the network forward, but through a different mechanism. Instead of adding the input activation to the output of the non-linear transformation, feature-maps from earlier in the network are simply passed as additional parameters.
In the original paper, this connectivity pattern is refered to as Dense Connectivity [1]. The chief advantage of this dense connectivity is that there is no summation operation involved in the information flow from earlier to later layers.
Normally in a convolutional neural network the dimensions of each feature map decreases as information flows through the network. However if the outputs of every layer are concatenated into a single tensor, the dimensions must remain the same so that the math continues to work out. Therefore the DenseNet architecture is broken down into Dense Blocks, in which the dense connectivity described above is used, followed by transition layers where the dimensions of the feature maps are reduced. An overview of this network architecture can be seen below.

Dense Blocks
Each dense block is composed of dense layers. The output of each dense layer is concatenated with the input of that layer to form a single tensor input for the next dense layer. Although there isn't a particular mathematical reason for it (at least none that I'm aware of) the paper describes each dense layer as producing a consistent number of feature maps. The number of feature maps produced by each layer is know as the growth rate. From the paper:
If each function produces feature-maps, it follows that the layer has input feature-maps, where is the number of channels in the input layer. ... We refer to the hyperparameter as the growth rate of the network [1].
For example, consider growth rate of 5 and an initial input with 3 channels. The first dense layer produces 5 additional channels which are concatenated with the initial input for a total of 8 channels. The second layer produces another 5 which means the input to the third layer will have 8 + 5 = 13 channels. This continues for the number of layers in the block.
The dense layer itself is composed of two steps. Each step is composed of three substeps: a batch normalization, rectified linear unit, and a convolution. In the first step the convolution is a 1x1 convolution and in the second step the convolution is a 3x3 convolution with 1 padding. These choices are deliberate. The first step reduces the total number of feature maps that are passed to the 3x3 convolution, which helps with keep the number of computations (and therefore the training time) low. The second step performs a traditional convolution while preserving the size of the remaining feature maps so that the output feature maps can be concatenated with the input feature maps.
Here is an implementation of a dense layer in PyTorch.
Note that the temp variable below can be modified however you like.
It's currently set to 4 times the growth rate because that's what the original authors used.
In our experiments, we let each 1x1 convolution produce 4k feature-maps [1].
"""model.py"""
class DenseLayer(nn.Module):
def __init__(self, num_input_maps: int, growth_rate: int):
super().__init__()
temp = 4 * growth_rate
# The 1x1 "conv"
self.batch_norm1 = nn.BatchNorm2d(num_features=num_input_maps)
self.relu1 = nn.ReLU()
self.conv1 = nn.Conv2d(
in_channels=num_input_maps,
out_channels=temp,
kernel_size=1,
stride=1,
padding=0,
bias=True,
)
# The 3x3 "conv"
self.batch_norm2 = nn.BatchNorm2d(num_features=temp)
self.relu2 = nn.ReLU()
self.conv2 = nn.Conv2d(
in_channels=temp,
out_channels=growth_rate,
kernel_size=3,
stride=1,
padding=1,
bias=True,
)
def forward(self, x):
x = self.batch_norm1(x)
x = self.relu1(x)
x = self.conv1(x)
x = self.batch_norm2(x)
x = self.relu2(x)
x = self.conv2(x)
return x
Now that we have an implementation of a dense layer we can use that to implement a dense block.
This step is actually quite simple.
The only tricky part is that the number of dense layers is variable.
Therefore each dense block will take in the number of dense layers as a parameter when it is initialized.
Then we can create the specified number of dense layers and add them to a list for processing.
Note that using a normal Python list won't work here.
The reason is that PyTorch doesn't have of including modules listed in a normal list in the computation graph.
We make use of the nn.ModuleList class from PyTorch, which will properly register the dense layers we store in it.
"""model.py"""
class DenseBlock(nn.Module):
def __init__(self, num_initial_maps: int, growth_rate: int, num_layers: int):
super().__init__()
self.num_initial_maps = num_initial_maps
self.growth_rate = growth_rate
self.num_layers = num_layers
# Since the number of layers is determined at run time we will generate
# a list of them to loop over for each forward call.
self.layers = nn.ModuleList()
for i in range(self.num_layers):
self.layers.append(
DenseLayer(
num_input_maps=(num_initial_maps + i*growth_rate),
growth_rate=growth_rate,
)
)
self.num_output_maps = self.num_initial_maps + self.num_layers * self.growth_rate
def forward(self, x):
for i in range(self.num_layers):
# Concatenate along dimension 1 since dimension 1 corresponds to channels
x = torch.cat((x, self.layers[i](x)), dim=1)
return x
Transition Layers
Transition layers sit between dense blocks and reduce the dimensions of feature maps. Note that there is no ReLU in the transition blocks.
The transition layers used in our experiments consist of a batch normalization layer and an 1x1 convolutional layer followed by a 2x2 average pooling layer [1].
These transition layers also include an optional parameter which can be used to reduce the number of feature maps the transition layer produces. must be greater than 0 and less than or equal to 1. We use because memory and compute speed isn't really an issue, so reducing the number of feature maps isn't necessary.
If a dense block contains m feature-maps, we let the following transition layer generate [theta m] output feature-maps, where 0 < theta <= 1 is referred to as the compression factor. When theta = 1, the number of feature- maps across transition layers remains unchanged.
"""model.py"""
class TransitionLayer(nn.Module):
def __init__(self, num_input_maps: int, theta: float = 1):
super().__init__()
self.num_output_maps = num_input_maps + int(num_input_maps * theta)
self.batch_norm = nn.BatchNorm2d(num_features=num_input_maps)
self.conv = nn.Conv2d(
in_channels=num_input_maps,
out_channels=self.num_output_maps,
kernel_size=1,
stride=1,
padding=0,
bias=True,
)
self.max_pool = nn.AvgPool2d(kernel_size=2, stride=2)
def forward(self, x):
x = self.batch_norm(x)
x = self.conv(x)
x = self.max_pool(x)
return x
The Classification Layer
The final layer in the DenseNet architecture is the classification layer. It is comprised of a global average pool and a fully connected layer with 120 classes.
"""model.py"""
class ClassificationLayer(nn.Module):
def __init__(self, num_input_maps, num_classes):
super().__init__()
self.average_pool1 = nn.AvgPool2d(kernel_size=7)
self.fully_connected1 = nn.Linear(in_features=num_input_maps, out_features=num_classes)
def forward(self, x):
x = self.average_pool1(x)
x = self.fully_connected1(torch.squeeze(x))
return x
Full Model
Now that the dense layers, dense blocks, transition layers, and classification layer have all been discussed we can implement the full DenseNet-XXX architecture by combining these smaller building blocks. Each DenseNet-XXX architecture has 4 dense blocks. The DenseNet-XXX variants simply change the number of dense layers in each block. For example, here is the breakdown for DenseNet-121.
- Initial Convolution Layer
- Dense Block 1: 6 dense layers
- Transition Layer 1
- Dense Block 2: 12 dense layers
- Transition Layer 2
- Dense Block 3: 24 dense layers
- Transition Layer 3
- Dense Block 4: 16 dense layers
- Classification Layer
The number at the end of the DenseNet-XXX refers to the number of layers in the model. In DenseNet-121 there are (6 + 12 + 24 + 16)*2 + 3 + 1 + 1 = 121 layers (two convolutions per dense layer, transition layers, initial convolution layer, and final classification layer).
We will use 32 for the growth rate and 64 filters in the initial convolution layer because that's what the original authors used in their paper. The number of feature maps in ever subsequent layer can then be calculated from these initial settings. The default number of layers in each dense block will create the DenseNet-121 model.
Notice that the output of this model is just the 120 activations from the fully connected layer in the ClassificationLayer. The loss function is addressed in more detail in the training section.
"""model.py"""
# Change these constants based on what model you are using
NUM_CLASSES = 120 # The Stanford Dogs Dataset has 120 classes of dogs in it.
class DenseNetModel(nn.Module):
def __init__(
self,
growth_rate: int = 32,
num_layers_dense_block_1: int = 6,
num_layers_dense_block_2: int = 12,
num_layers_dense_block_3: int = 24,
num_layers_dense_block_4: int = 16,
theta_1: float = 1,
theta_2: float = 1,
theta_3: float = 1,
):
super().__init__()
temp = 2 * growth_rate
self.conv1 = nn.Conv2d(in_channels=3, out_channels=temp, kernel_size=7, stride=2, padding=3, bias=True)
self.max_pool1 = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
self.dense_block1 = DenseBlock(
num_initial_maps=temp,
growth_rate=growth_rate,
num_layers=num_layers_dense_block_1,
)
self.transition_layer1 = TransitionLayer(
num_input_maps=self.dense_block1.num_output_maps,
theta=theta_1,
)
self.dense_block2 = DenseBlock(
num_initial_maps=self.transition_layer1.num_output_maps,
growth_rate=growth_rate,
num_layers=num_layers_dense_block_2,
)
self.transition_layer2 = TransitionLayer(
num_input_maps=self.dense_block2.num_output_maps,
theta=theta_2,
)
self.dense_block3 = DenseBlock(
num_initial_maps=self.transition_layer2.num_output_maps,
growth_rate=growth_rate,
num_layers=num_layers_dense_block_3,
)
self.transition_layer3 = TransitionLayer(
num_input_maps=self.dense_block3.num_output_maps,
theta=theta_3,
)
self.dense_block4 = DenseBlock(
num_initial_maps=self.transition_layer3.num_output_maps,
growth_rate=growth_rate,
num_layers=num_layers_dense_block_4,
)
self.classification_layer = ClassificationLayer(
num_input_maps=self.dense_block4.num_output_maps,
num_classes=NUM_CLASSES,
)
def forward(self, x):
x = self.conv1(x)
x = self.max_pool1(x)
x = self.dense_block1(x)
x = self.transition_layer1(x)
x = self.dense_block2(x)
x = self.transition_layer2(x)
x = self.dense_block3(x)
x = self.transition_layer3(x)
x = self.dense_block4(x)
x = self.classification_layer(x)
return x
The Dataset
The model will be trained on the Stanford Dogs Dataset, which contains 20,580 images categorized into 120 classes of dogs [2]. Here is two example images from the dataset of an African hunting dog and a Brabancon Griffon.


The dataset can be downloaded as a tarball from the Stanford Dogs Dataset website. If you have an SSD available, you should save the images on it. This will decrease the amount of time spent waiting for images to be loaded from disk before being passed into the network. Here is an example of getting the images.
mkdir ~/Datasets
cd ~/Datasets
curl -O http://vision.stanford.edu/aditya86/ImageNetDogs/images.tar
tar xf ./images.tar
The extracted images will be stored in a newly created directory called Images. Within the images directory there are 120 subdirectories, each corresponding to a specific breed of dog. I've included a snippet of the Images directory as well as one of the subdirectories below.
(venv) nthomas@theodore:~$ ls -l ~/Datasets/Stanford\ Dogs\ Dataset/Images/
total 1440
drwxr-xr-x 2 nthomas nthomas 12288 Oct 9 2011 n02085620-Chihuahua
drwxr-xr-x 2 nthomas nthomas 12288 Oct 9 2011 n02085782-Japanese_spaniel
drwxr-xr-x 2 nthomas nthomas 12288 Oct 9 2011 n02085936-Maltese_dog
drwxr-xr-x 2 nthomas nthomas 12288 Oct 9 2011 n02086079-Pekinese
drwxr-xr-x 2 nthomas nthomas 12288 Oct 9 2011 n02086240-Shih-Tzu
drwxr-xr-x 2 nthomas nthomas 12288 Oct 9 2011 n02086646-Blenheim_spaniel
...
(venv) nthomas@theodore:~$ ls -l ~/Datasets/Stanford\ Dogs\ Dataset/Images/n02116738-African_hunting_dog/
total 6992
-rw-r--r-- 1 nthomas nthomas 16375 Oct 9 2011 n02116738_10024.jpg
-rw-r--r-- 1 nthomas nthomas 5898 Oct 9 2011 n02116738_10038.jpg
-rw-r--r-- 1 nthomas nthomas 20344 Oct 9 2011 n02116738_10081.jpg
-rw-r--r-- 1 nthomas nthomas 10662 Oct 9 2011 n02116738_10169.jpg
-rw-r--r-- 1 nthomas nthomas 11780 Oct 9 2011 n02116738_10215.jpg
-rw-r--r-- 1 nthomas nthomas 51252 Oct 9 2011 n02116738_10469.jpg
-rw-r--r-- 1 nthomas nthomas 14459 Oct 9 2011 n02116738_10476.jpg
This type of layout for images is extremely common in computer vision and it means that we can leverage PyTorch's ImageFolder dataset to load the images easily.
The code snippet below shows how you can create training and validation DataLoaders from this extracted directory.
Note that the images are not all 224x224, which means that we will need to resize the images as they are loaded from the disk.
This is necessary because our model expects the input images to be 224x224.
The training DataLoader includes additional transforms from the torchvision packages to increase the perceived size of the training set.
This data augmentation also helps reduce model overfitting.
Additionally, note the presense of the torch.manual_seed(seed) call.
This sets the seed PyTorch uses for randomization so that the training / validation split is always the same.
Since the training validation split is always the same, it's possible to stop and resume training knowing that the next time you create the DataLoaders they will be the same.
"""data.py"""
import torch
from torch.utils.data import random_split, DataLoader, Subset
from torchvision.datasets import ImageFolder
from torchvision.transforms import v2
def get_dataloaders(filepath: str, batch_size: int = 1, seed=10):
torch.manual_seed(seed)
# Define transforms for both datasets. Data augmentation is only done on the
# training set
train_transforms = v2.Compose([
v2.Resize((255, 255)),
v2.RandomRotation(30),
v2.RandomResizedCrop((224, 224)),
v2.RandomHorizontalFlip(),
v2.ToImage(),
v2.ToDtype(torch.float32, scale=True),
v2.Normalize(mean=(0.5, 0.5, 0.5), std=(0.5, 0.5, 0.5)),
])
val_transforms = v2.Compose([
v2.Resize((255, 255)),
v2.CenterCrop((224, 224)),
v2.ToImage(),
v2.ToDtype(torch.float32, scale=True),
v2.Normalize(mean=(0.5, 0.5, 0.5), std=(0.5, 0.5, 0.5)),
])
# Both datasets load images from the same data root. They will be split
# based on their indices later.
train_dataset = ImageFolder(
filepath,
transform=train_transforms,
)
val_dataset = ImageFolder(
filepath,
transform=val_transforms,
)
# Reserve 10% of the dataset for validation
indices = torch.arange(len(train_dataset))
train_indices, val_indices = random_split(indices, [0.9, 0.1])
train_subset = Subset(train_dataset, train_indices)
val_subset = Subset(val_dataset, val_indices)
train_loader = DataLoader(train_subset, batch_size=batch_size, shuffle=True)
val_loader = DataLoader(val_subset, batch_size=batch_size, shuffle=True)
return train_loader, val_loader
Training
The actual training loop is pretty straighforward. It follows the same steps any other deep learning algorithm uses:
- Compute the forward pass
- Compute the loss and accuracy
- Compute the gradients
- Update the parameters
Since this is a multi-class classification problem we will use cross entropy as the loss function. Here is the loop implemented in Python. This loop is used for both the training and validation passes. The main difference is that on validation passes we do not track the gradients or update parameters.
"""loop.py"""
import time
import numpy as np
import torch
import torch.nn.functional as F
def loop(
is_train: bool,
model,
optimizer,
loss_fn, # a nn.CrossEntropyLoss should be passed for this parameter
loader,
device,
history,
):
start = time.time()
num_correct = 0
losses = np.zeros(len(loader))
mode = "training" if is_train else "validation"
for idx, mini_batch in enumerate(loader):
print(f"\t{mode} index: {idx}", end='\r')
if is_train:
model.train()
else:
model.eval()
images = mini_batch[0].to(device)
labels = mini_batch[1].to(device)
# Only track the gradients if the loop is a training loop. We don't
# need to track gradients during a validation loop since no backward
# pass is performed. This saves memory and speeds up the forward pass.
with torch.set_grad_enabled(is_train):
# Step 1: Forward pass
yhat = model(images)
# Step 2: Compute loss and accuracy
loss = loss_fn(yhat, labels)
losses[idx] = loss.item()
# torch.max returns a tensor with two parameters: raw values and the
# index of the raw values. The [-1] returns the index.
predicted = torch.max(
F.softmax(yhat, dim=-1),
-1,
)[-1]
num_correct += (predicted == labels).sum().item()
if is_train:
# Step 3: Compute gradients
loss.backward()
# Step 4: Update parameters
optimizer.step()
optimizer.zero_grad()
history["loss"].append(np.mean(losses))
history["accuracy"].append(num_correct / (len(loader) * loader.batch_size))
print(f"\n\t\t{mode} loss: {history['loss'][-1]:.2f}")
print(f"\t\t{mode} accuracy: {history['accuracy'][-1]:.2f}")
end = time.time()
print(f"\t\t{mode} loop time: {end - start:.2f} seconds")
We are almost ready to begin training. However before we start it would be nice to have a method of saving our progress so that training can be stopped and resumed if necessary. These two helper functions will save and load training checkpoints.
"""helpers.py"""
import torch
def load_checkpoint(model, optimizer, filepath: str = "model.pth"):
total_epochs = 0
training_history = {"loss": [], "accuracy": []}
validation_history = {"loss": [], "accuracy": []}
try:
loaded_checkpoint = torch.load(filepath)
model.load_state_dict(loaded_checkpoint["model_state_dict"])
optimizer.load_state_dict(loaded_checkpoint["optimizer_state_dict"])
total_epochs = loaded_checkpoint["total_epochs"]
training_history = loaded_checkpoint["training_history"]
validation_history = loaded_checkpoint["validation_history"]
print(
f"Loaded checkpoint successfully. Previously completed {total_epochs} epochs."
)
return total_epochs, training_history, validation_history
except Exception as e:
print("Unable to load checkpoint. Starting from scratch.")
print(f"The error was: {e}")
return total_epochs, training_history, validation_history
def save_checkpoint(checkpoint):
"""Save progress to continue training later"""
try:
checkpoint_name = (
f"model_{checkpoint['total_epochs']}-epochs.pth"
)
torch.save(checkpoint, checkpoint_name)
torch.save(checkpoint, "model.pth")
print("Successfully saved checkpoint.")
except Exception as e:
print("Unable to save checkpoint.")
print(f"The error was: {e}")
Finally we can start training.
Here is the full code for training the model.
It's started with python train.py --epochs 300 --batch-size 8.
"""train.py"""
import time
import arg_parser
import data
import helpers as h
from loop import loop
from model import DenseNetModel
import torch
from torch import nn, optim
def main():
parser = arg_parser.create_parser()
args = parser.parse_args()
train_loader, val_loader = data.get_dataloaders(
args.dataset_file_path,
args.batch_size,
)
device = "cuda" if torch.cuda.is_available() else "cpu"
print(f"Using device: {device}\n")
model = DenseNetModel().to(device)
criterion = nn.CrossEntropyLoss().to(device)
optimizer = optim.Adam(model.parameters(), lr=args.learning_rate)
total_epochs, training_history, validation_history = h.load_checkpoint(
model=model,
optimizer=optimizer,
)
print(f"\nUsing batch size: {args.batch_size}")
print(f"Size of training data loader is: {len(train_loader)}")
print(f"Size of validation data loader is: {len(val_loader)}")
print(f"Performing {args.epochs} epochs\n")
all_start = time.time()
for epoch in range(args.epochs):
print(f"Current epoch: {epoch + 1}")
epoch_start = time.time()
# Training
loop(
is_train=True,
model=model,
optimizer=optimizer,
loss_fn=criterion,
loader=train_loader,
device=device,
history=training_history,
)
# Validation
loop(
is_train=False,
model=model,
optimizer=optimizer,
loss_fn=criterion,
loader=val_loader,
device=device,
history=validation_history,
)
epoch_end = time.time()
total_epochs += 1
print(f"Total epoch time: {epoch_end - epoch_start:.2f} seconds\n")
# Save model every 10 epochs
if total_epochs % 10 == 0:
checkpoint = {
"total_epochs": total_epochs,
"model_state_dict": model.state_dict(),
"optimizer_state_dict": optimizer.state_dict(),
"training_history": training_history,
"validation_history": validation_history,
}
h.save_checkpoint(checkpoint)
all_end = time.time()
print(f"Total training time for {args.epochs} epochs: {all_end - all_start:.2f} seconds\n")
checkpoint = {
"total_epochs": total_epochs,
"model_state_dict": model.state_dict(),
"optimizer_state_dict": optimizer.state_dict(),
"training_history": training_history,
"validation_history": validation_history,
}
h.save_checkpoint(checkpoint)
h.plot_histories(training_history, validation_history)
if __name__ == "__main__":
main()
Results
Training was performed on an NVIDIA GeForce RTX 4060 Ti. During training the program used 4516MiB of memory when using a batch size of 8 for both training and validation.
Fri Feb 16 22:07:48 2024
+-----------------------------------------------------------------------------+
| NVIDIA-SMI 525.147.05 Driver Version: 525.147.05 CUDA Version: 12.0 |
|-------------------------------+----------------------+----------------------+
| GPU Name Persistence-M| Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap| Memory-Usage | GPU-Util Compute M. |
| | | MIG M. |
|===============================+======================+======================|
| 0 NVIDIA GeForce ... Off | 00000000:01:00.0 On | N/A |
| 48% 69C P2 123W / 165W | 5909MiB / 16380MiB | 99% Default |
| | | N/A |
+-------------------------------+----------------------+----------------------+
+-----------------------------------------------------------------------------+
| Processes: |
| GPU GI CI PID Type Process name GPU Memory |
| ID ID Usage |
|=============================================================================|
...
| 0 N/A N/A 2739019 C python 4516MiB |
+-----------------------------------------------------------------------------+
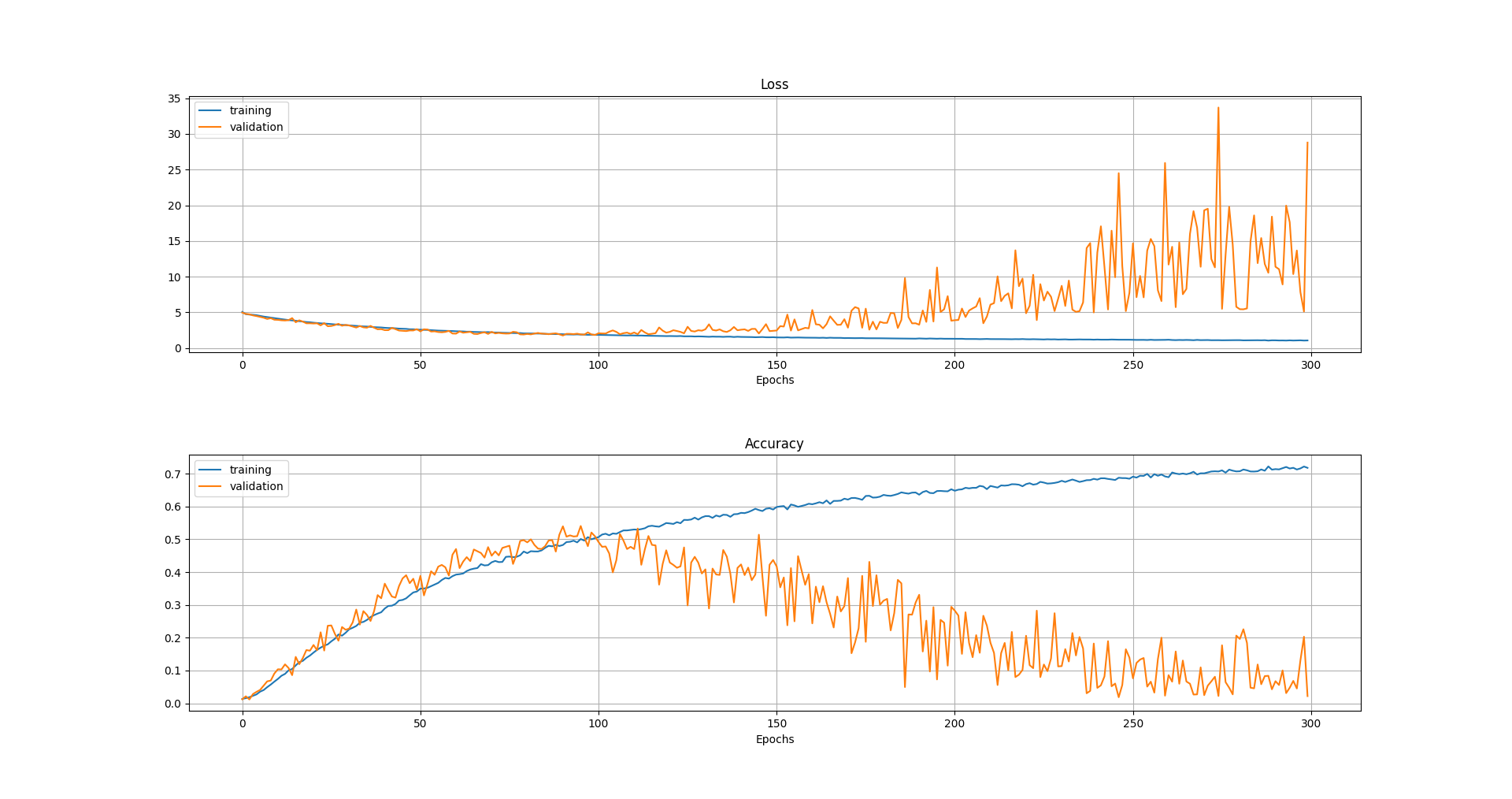
Accuracy and loss on the training set continued to improve throughout the training (as expected). However the validation set began seeing a decrease in accuracy and increase in loss around 100 epochs. Therefore this is the point in which the model begins to overfit to the training dataset. Accuracy peaks at about 50%. That number is a little dissapointing, but it's a lot better than I would be able to perform. Additionally it beats the 22% accuracy achieved in the original experiments on this dataset [2].
If you want to validate or use any of this code yourself you can find it in my GitLab repository. The checkpoints aren't saved in GitLab but you can download checkpoints from 100 epochs and the full 300 epochs on my website.
References
[1] Densely Connected Convolutional Networks
[2] Aditya Khosla, Nityananda Jayadevaprakash, Bangpeng Yao and Li Fei-Fei. Novel dataset for Fine-Grained Image Categorization. First Workshop on Fine-Grained Visual Categorization (FGVC), IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2011.
[3] PyTorch Team. PyTorch: An Imperative Style, High-Performance Deep Learning Library