Inverted Point Mass Equations of Motion

Problem Description

Pendulum On A Cart

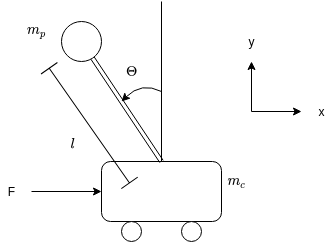
Say we are given an inverted point mass on a cart as shown above. The mass of the cart is $m_{c}$ . The mass of the point at the end of the rod is $m_{p}$ . The rod is length $l$ , rigid, and massless. And external force $F$ is applied in the positive $x$ direction. The system coordinates are shown. We wish to find the equations of motion describing this system. There are two commonly used approaches: Newtonian Mechanics and Lagrangian Mechanics.

Note: This problem is different from an inverted pendulum in that it does not consider the mass or moment of inertia of the rod. The approach for an inverted pendulum is very similar.

Newtonian

Pendulum FBD Cart FBD

Newtonian mechanics is all about summing the forces acting on an object. Therefore we need to make two free body diagrams (FBDs). One for the point mass and one for the cart.

Now we can apply Newton's second law to the point mass. Here $a_{p}$ is the pendulum acceleration. First we look in horizontal direction.

\begin{align} \sum F_{\hat{\imath}} &= m_{p}a_{p,\hat{\imath}}\\\\ T\sin(\Theta) &= m_{p}a_{p,\hat{\imath}} \end{align}

Now we can look at the vertical direction on the pendulum.

\begin{aligned} \sum F_{\hat{\jmath}} &= m_{p}a_{p,\hat{\jmath}}\\\\ -T\cos(\Theta) - m_{p}g &= m_{p}a_{p,\hat{\jmath}} \end{aligned}

We can also do an analysis on the cart. Because the cart is constrained to move in the horizontal direction, no useful information is gained from summing the vertical forces. Therefore we will only do an analysis on the horizontal forces.

\begin{aligned} \sum F_{\hat{\imath}} &= m_{c}a_{c,\hat{\imath}}\\\\ -T\sin(\Theta) + F &= m_{c}\ddot{x} \end{aligned}

Now we have equations describing the motion of the cart and pendulum. However the equations are not written in terms of the system states, $\Theta$ and $x$ . Recall from physics that the acceleration of a point can be written in terms of relative acceleration. That is, the acceleration of the pendulum can be written as the acceleration of the cart plus the acceleration of the pendulum relative to the cart.

a_{p} = a_{c} + a_{p/c}

Now recall that the pendulum is fixed to the cart by a rigid rod. Therefore the pendulum can only move in a perfect circle around the cart as shown below.

Pendulum Motion

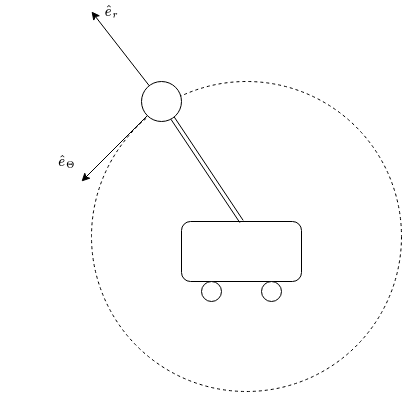
Now we can write the acceleration of the pendulum relative to the cart in terms of the tangential and centripetal accelerations. Here is a link to the Wikipedia page showing how the this relates to normal $x,y$ coordinates. This centripetal acceleration can be easily changed back to the $\Theta$ coordinates with simple trigonometry.

\begin{aligned} a_{p} &= a_{c} + a_{p/c}\\\\ a_{p} &= \ddot{x}\hat{\imath} + [l\ddot{\Theta}\hat{e}_{\Theta} - l \dot{\Theta}^{2}\hat{e}_{r}] \end{aligned}

These new coordinates can be transformed in terms of $\Theta$ through the use of some simple trigonometry. If you are confused recall that $\hat{e}_{r}$ is the same as the with the line drawn from the pivot on the cart to the point mass and that unit vectors have length 1. The above equation can be rewritten as the following.

\begin{aligned} a_{p} &= a_{c} + a_{p/c}\\\\ a_{p} &= \ddot{x}\hat{\imath} + [l\ddot{\Theta}\hat{e}_{\Theta} - l\dot{\Theta}^{2}\hat{e}_{r}] \\\\ a_{p} &= \ddot{x}\hat{\imath} + l\ddot{\Theta}(-\cos(\Theta)\hat{\imath} - \sin(\Theta)\hat{\jmath}) - l\dot{\Theta}^{2}(-\sin(\Theta)\hat{\imath} + \cos(\Theta)\hat{\jmath}) \end{aligned}

We can take this new expression for $a_{p}$ and substitute it into our equations for the horizontal and vertical forces on the pendulum. Note that we only add the $\hat{\imath}$ to the horizontal equations and only add the $\hat{\jmath}$ terms to the vertical equations.

First look at the horizontal.

\begin{aligned} T\sin(\Theta) &= m_{p}a_{p,\hat{\imath}}\\\\ T\sin(\Theta) &= m_{p}[\ddot{x} - l\ddot{\Theta}\cos(\Theta) + l\dot{\Theta}^{2}\sin(\Theta)] \end{aligned}

Now look at the vertical.

\begin{aligned} -T\cos(\Theta) - m_{p}g &= m_{p}a_{p,\hat{\jmath}}\\\\ -T\cos(\Theta) - m_{p}g &= m_{p}[-l\ddot{\Theta}\sin(\Theta) - l\dot{\Theta}^{2}\cos(\Theta)] \end{aligned}

Now we have everything written in terms of $\Theta$ and $x$ . However we have two system states and three unknown quantities: $x$ , $\Theta$ , and $T$ . This means we can reduce the number of equations we have. We will eliminate T because it isn't a system state.

Eliminating $T$ from the two pendulum equations is done with an addition trick. See the steps below.

\begin{aligned} \cos(\Theta)[\sum F_{\hat{\imath}} &= m_{p}a_{p,\hat{\imath}}]\\\\ +\sin(\Theta)[\sum F_{\hat{\jmath}} &= m_{p}a_{p,\hat{\jmath}}] \end{aligned}

\begin{aligned} T\sin(\Theta)\cos(\Theta) - T\sin(\Theta)\cos(\Theta) &- m_{p}g\sin(\Theta) \\\\ &= m_{p}\ddot{x}\cos(\Theta) - m_{p}l\ddot{\Theta}\cos^{2}(\Theta) \\\\ &+ m_{p}l\dot{\Theta}^{2}\sin(\Theta)\cos(\Theta) \\\\ &- m_{p}l\ddot{\Theta}\sin^{2}(\Theta) \\\\ &- m_{p}l\dot{\Theta}^{2}\cos(\Theta)\sin(\Theta)\\\\ \end{aligned}

\begin{aligned} -m_{p}g\sin(\Theta) &= m_{p}\ddot{x}\cos(\Theta) - m_{p}l\ddot{\Theta}\\\\ g\sin(\Theta) &= \ddot{x}\cos(\Theta) - l\ddot{\Theta}\\\\ \end{aligned}

l\ddot{\Theta} - \ddot{x}\cos(\Theta) - g\sin(\Theta) = 0

And we have our first equation of motion.

Now we have to eliminate $T$ from the cart equation. Luckily we already have an expression for $T\sin(\Theta)$ that we found while rewriting Newton's second law for the pendulum. Recall.

T\sin(\Theta) = m_{p}[\ddot{x} - l\ddot{\Theta}\cos(\Theta) + l\dot{\Theta}^{2}\sin(\Theta)]

This can be substituted into the cart equation to eliminate $T$ .

\begin{aligned} \sum F_{\hat{\imath}} &= m_{c}a_{c,\hat{\imath}}\\\\ -T\sin(\Theta) + F &= m_{c}\ddot{x}\\\\ -m_{p}[\ddot{x} - l\ddot{\Theta}\cos(\Theta) + l\dot{\Theta}^{2}\sin(\Theta)] + F &= m_{c}\ddot{x}\\\\ \end{aligned}

Which after some rearranging can be made to look like the following.

\ddot{x}(m_{c} + m_{p}) - m_{p}l\ddot{\Theta}\cos(\Theta) + m_{p}l\dot{\Theta}^{2}\sin(\Theta) = F

So our two equation of motion for this system are as follows.

\begin{equation} \ddot{x}(m_{c} + m_{p}) - m_{p}l\ddot{\Theta}\cos(\Theta) + m_{p}l\dot{\Theta}^{2}\sin(\Theta) = F \end{equation}

\begin{equation} l\ddot{\Theta} - \ddot{x}\cos(\Theta) - g\sin(\Theta) = 0 \end{equation}

Lagrangian

Similar to the Newtonian $F=ma$ , the fundamental equations in Lagrangian mechanics are the Lagrange equations.

\frac{d}{dt}\frac{\partial L}{\partial \dot{q_{i}}} - \frac{\partial L}{\partial q_{i}} = Q_{i}

Each $q_{i}$ is a coordinate of the system which in this case corresponds with $q_{1}=x$ and $q_{2} = \Theta$ . The Lagrangian, $L$ , is given by the following.

L = T - V

Where $T$ is the kinetic energy of the system and $V$ is the potential energy of the system.

Because the cart is constrained to move only in the x direction there is no potential energy in the system due to the cart. The potential energy is given by the location of the point mass at the end of the rod.

V = m_{p}gh = m_{p}gl\cos(\Theta)

The kinetic energy is a little more complicated because the cart does contribute to the total kinetic energy. Therefore the kinetic energy is given by the following.

\begin{aligned} T &= T_{c} + T_{p}\\\\ T &= \frac{1}{2}m_{c}\dot{x}^{2} + \frac{1}{2}m_{p}v_{p}^{2}\\\\ T &= \frac{1}{2}m_{c}\dot{x}^{2} + \frac{1}{2}m_{p}(v_{p,x}^{2} + v_{p,y}^{2})\text{ By The Pythagorean Theorem}\\\\ T &= \frac{1}{2}m_{c}\dot{x}^{2} + \frac{1}{2}m_{p}[(\dot{x}-l\dot{\Theta}\cos(\Theta))^{2} + (-l\dot{\Theta}\sin(\Theta))^{2}]\\\\ T &= \frac{1}{2}m_{c}\dot{x}^{2} +\frac{1}{2}m_{p}[\dot{x}^{2} - 2l\dot{x}\dot{\Theta}\cos(\Theta) + l^{2}\dot{\Theta}^{2}\cos^{2}(\Theta) + l^{2}\dot{\Theta}^{2}\sin^{2}(\Theta)]\\\\ T &= \frac{1}{2}\dot{x}^{2}(m_{c} + m_{p}) + \frac{1}{2}m_{p}[-2l\dot{x}\dot{\Theta}\cos(\Theta) + l^{2}\dot{\Theta}^{2}]\\\\ T &= \frac{1}{2}\dot{x}^{2}(m_{c} + m_{p}) - m_{p}l\dot{x}\dot{\Theta}\cos(\Theta) + \frac{1}{2}m_{p}l^{2}\dot{\Theta}^{2} \end{aligned}

Therefore the total Lagrangian can be expressed as follows.

\begin{aligned} L &= T - V\\\\ L &= (\frac{1}{2}\dot{x}^{2}(m_{c} + m_{p}) - m_{p}l\dot{x}\dot{\Theta}\cos(\Theta) + \frac{1}{2}m_{p}l^{2}\dot{\Theta}^{2}) - (m_{p}gl\cos(\Theta)) \end{aligned}

Now we only need to solve the Lagrange equations for each of the two coordinates, $x$ and $\Theta$ . We will end up with two equations of motion, which is what we should expect for a system with two degrees of freedom. The first is the equation for the $x$ coordinate.

\begin{aligned} F &= \frac{d}{dt}\frac{\partial L}{\partial \dot{x}} - \frac{\partial L}{\partial x}\\\\ F &= \frac{d}{dt}(\dot{x}(m_{c} + m_{p}) - m_{p}l\dot{\Theta}\cos(\Theta)) - (0) \\\\ F &= \ddot{x}(m_{c} + m_{p}) - m_{p}l\ddot{\Theta}\cos(\Theta) + m_{p}l\dot{\Theta}^{2}\sin(\Theta) \end{aligned}

Now we can do it again with the $\Theta$ coordinate.

\frac{d}{dt}\frac{\partial L}{\partial \dot{x}} - \frac{\partial L}{\partial x} = 0

\frac{d}{dt}(-m_{p}l\dot{x}\cos(\Theta) + m_{p}l^{2}\dot{\Theta}) - (m_{p}l\dot{x}\dot{\Theta}\sin(\Theta) + m_{p}gl\sin(\Theta)) = 0

-m_{p}l\ddot{x}\cos(\Theta) + m_{p}l\dot{x}\dot{\Theta}\sin(\Theta) + m_{p}l^{2}\ddot{\Theta} - (m_{p}l\dot{x}\dot{\Theta}\sin(\Theta) + m_{p}gl\sin(\Theta)) = 0

$l\ddot{\Theta} - \ddot{x}\cos(\Theta) - g\sin(\Theta) = 0$

So our two equations of motion are written below. You can see the match the ones found for the Newtonian formulation exactly. This is what we should expect as they describe the same system.

$\begin{equation} \ddot{x}(m_{c} + m_{p}) - m_{p}l\ddot{\Theta}\cos(\Theta) + m_{p}l\dot{\Theta}^{2}\sin(\Theta) = F \end{equation}$

$\begin{equation} l\ddot{\Theta} - \ddot{x}\cos(\Theta) - g\sin(\Theta) = 0 \end{equation}$